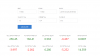
The reasons due to which the deltas of the ATM call and put are different, as shown in your screenshot is because:
- The calculator that Zerodha uses is based on the BSM model. It means that the interest rate that you input is used by the model to calculate a forward price for the stock. The model then uses that forward price (and not the stock price that you input) as the underlying price. Going by this, the higher the interest rate and more time to remaining, the higher would be the call price and lower the put price and different deltas. This should be simple.
On a side note, the theoretical premium (in the screenshot) for the 11500 call and put is different. Hence, once can easily tell that it is the Black-Scholes-Merton (BSM) model.
- In addition to this, even if the model did not calculate the forward price (such as the Black76 model) and took the forward price as the actual input, it would show the deltas of the ATM calls and put different.
Why?
Because if you look at what the delta calculation formula for a call, it is: Exp(-1 * riskfree_rate * time_to_expiration) * N(d1) and for a put it is: : Exp(-1 * riskfree_rate * time_to_expiration) * N(d1-1)
Here N(x) is the standard cumulative normal distribution function. It returns the probability of getting an occurrence less than x by calculating the area under the standard normal distribution curve between the values of –∞ and x
d1 = tells us, in standard deviations, how far the exercise price is from the mean. This means that
if in case, d1 = 0.5, then the absolute delta would be same for both the ATM call and put. But is d1 equal to 0.5 for ATM strike?
Thought it may seem that for an ATM option, d1 should be exactly half, but the caveat here is that stock prices do not follow normal distribution, but rather the log-normal distribution. There is a slight upward drift in Geometric Brownian motion.
To elaborate more, the actual formula for d1 that we use in option modelling is (ln(S/K)+(r+0.5σ* σ)(t))/σ√t
This is already adjusted for log-normal distribution ( by adding (0.5σ* σ*t) ). Hence d1 is slightly greater than 0.5 (used for call delta) and naturally, (d1 - 1) which is used for the put delta calculation, is slightly less than 0.5 irrespective of the model used.
As an example, here are the greeks calculated for your inputs in Black76 (suitable for Indian markets):
Call:
array (size=6)
'delta' => float 0.50614867659299
'gamma' => float 0.00074208045206883
'vega' => float 14.116047503481
'theta' => float -2.9877335075589
'rho' => float -0.20307554867875
'premium' => float 211.77878647927
Put:
array (size=6)
'delta' => float -0.48773312994262
'gamma' => float 0.00074208045206883
'vega' => float 14.116047503481
'theta' => float -2.9877335075589
'rho' => float -0.20307554867875
'premium' => float 211.77878647927
Note that while using the Black76 model, it shows the premium as same for both the call and put because we have input the strike as 11500 and the forward price as 11500 as well. However, the deltas are still different. Hope this helps.